I did this research project at Systems Group, ETH, advised by Prof. Dr. Gustavo Alonso.
1. Highlights: efficient priority queue
In this project, the most important thing is to realize a priority queue with size 128. The target is to ensure that the interval of inserting into this queue matches the speed of random memory access (4~5 cycles). Besides, the latency of single insertion should be as small as possible. Traditionally, I can build priority queue with tree structure. I need to compare log(128)=7 times and then do element movements. Operations can be pipelined but the latency of moving elements is too high.
To solve this problem, I build a priority queue with out-of-order storage. Each element has two registers, one for data, the other for index (representing the priority). The operation of each element is independent of each other. The input would compare with the data of all elements simultaneously. Then according to the result of comparison, the index of each element would increase or keep the same. Next, I would construct a bitmap according to these indexes. The original index of all elements ranges from 0~127. When a new element is inserted into the queue, some indexes keep the same while the other indexes are incremented by 1. This means for the range of 0~127 (the element with index 128 is discarded), there would be one vacant position and it is used to be the index of the new element. The dataflow is shown as below:
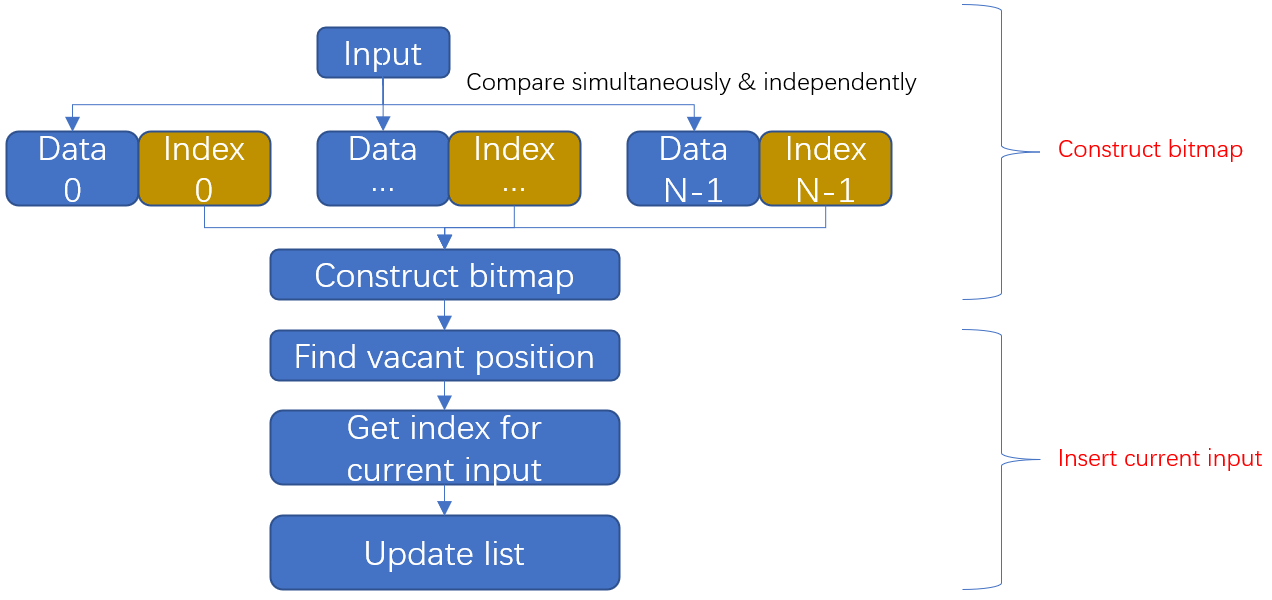
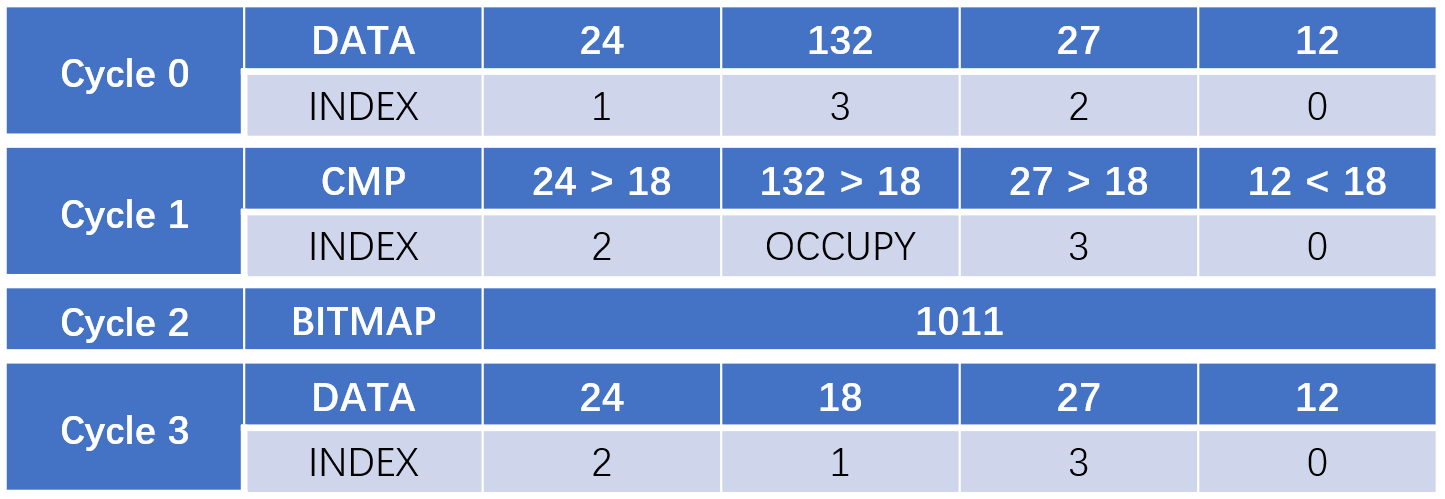
Assuming the queue size is 4 and the new input is 18, operations per cycle are shown as below:
However, the interval of such design is a bit high due to the "selection" operation. To help reduce the interval, I manage to split the whole process into two independent stages. As a result, the throughput of consecutive insertion is maximized by pipelining bitmap construction and queue update. The dataflow is shown as below:
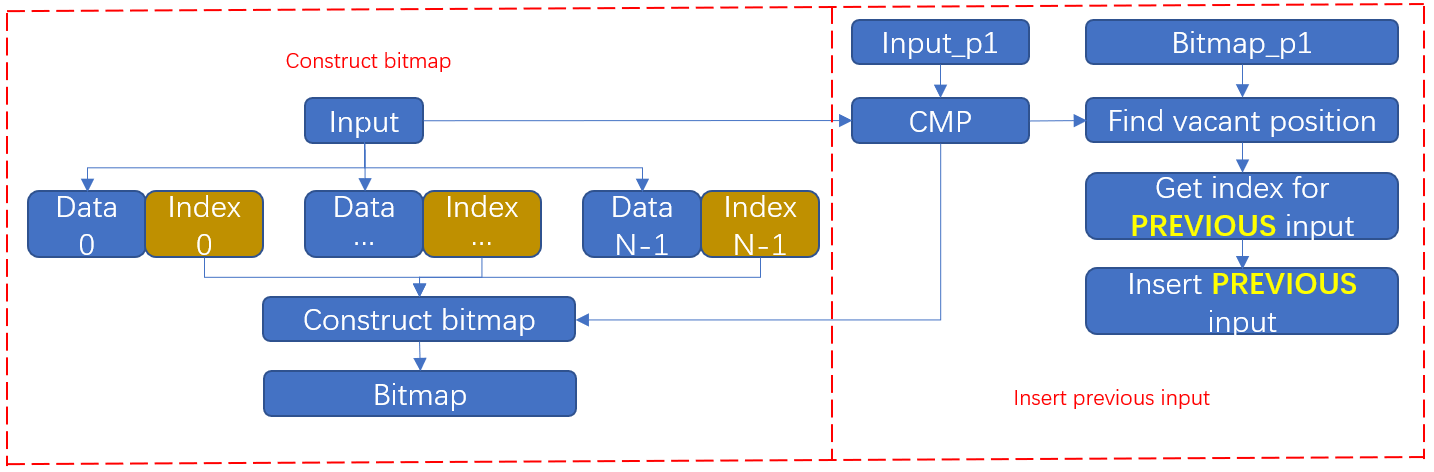
Still assuming the queue size is 4 and the new input is 18, operations per cycle are shown as below:
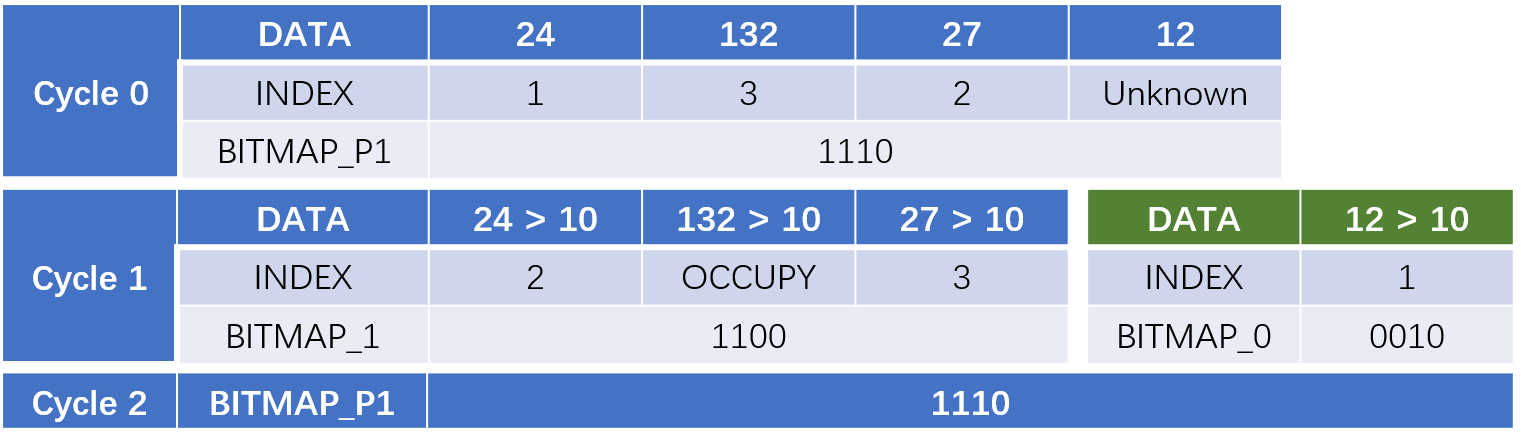
Finally, the initiation interval of inserting into priority queue matches the speed of random memory access. And the latency of single insertion is ignorable.
2. Introduction:
Nearest-Neighbor-Search (NNS) problem means given a query vector and a defined distance function, it requires to return the node among the whole dataset which has the nearest distance with the query vector. Such exact solution is time-consuming. So that Approximate-Nearest-Neighbor-Search (ANNS) relaxes the condition of exact search and allows a small number of errors. Researchers use "recall" to measure the quality of inexact search. The common definition of "recall" is the ratio for all query vectors whether the true nearest neighbor is found in the returned K nodes.
To help accelerate ANNS in large dataset, Malkov proposed Hierarchical-Navigable-Small-World model (HNSW) based on proximity graph algorithm. In this model, it has several layers and each node is assigned a different maximum layer according to exponential distribution. The search always starts from the top layer with a random enter node. It would go to the next layer when it reaches the node with minimum distance with the query vector. The basic structure of HNSW is shown as below:
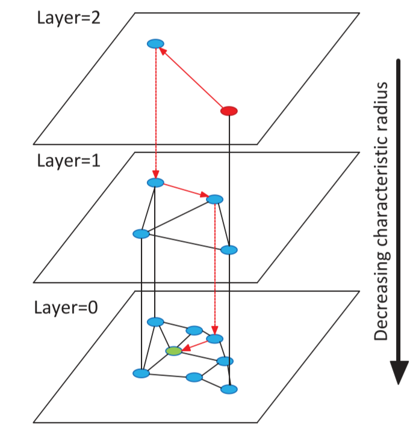
3. Analysis:
FPGA has good performance when operations can be fully pipelined and parallelized. But for graph algorithm such as HNSW, new search depends on the output of the last search so that I cannot fully pipeline these operations. Random memory access is the other bottleneck. The comparison of throughput (query per second) between FPGA and CPU is shonw as below:
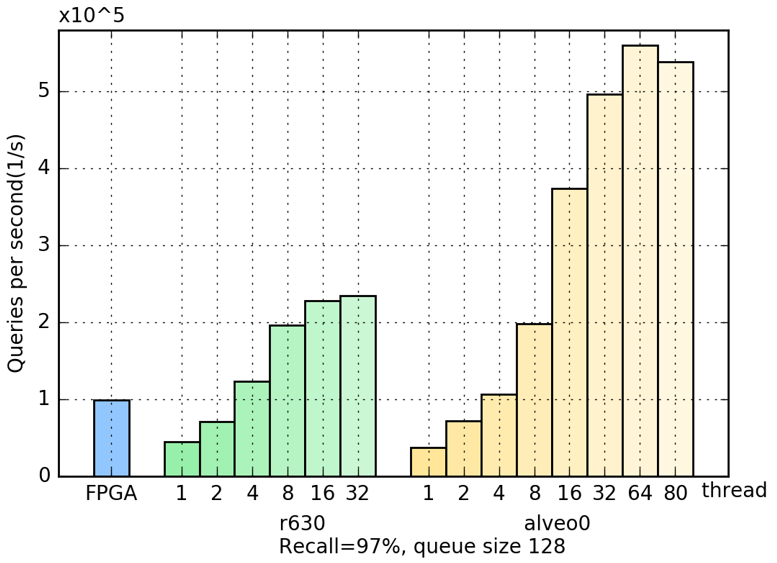
The FPGA in use is Alveo U280 (32 HBM channels, running frequency 130MHz). CPUs for comparison are R630 (32 cores) and Alveo0 (80 cores).
All the codes are written in HLS. For more details, please contact me.